The difference between area and perimeter is the area is defined by the region occupied by shape and therefore the perimeter can be defined as the length of the outer boundary of the shape. Both the terms define the size of a shape. Learn more on perimeter and area here. One can easily get confused between these terms which look similar but have an enormous difference between them. Here we are going to discuss the essential differences and a few of the fundamental features and calculate the Area & Perimeter for those shapes.
What is Area?
The area is that the region bounded by the form of an object. The space covered by the figure or any geometric shape is that the area of the shape. The area of all the shapes depends upon their dimensions and properties. Different shapes have different areas. The area of the square is different from the area of the kite.
If two objects have a similar shape then the area covered by them doesn’t have to be equal unless and until the size of both shapes is also equal. Suppose there are two rectangle boxes with the length as L1 and L2 and breadth as B1 and B2. So the rectangular box areas say, A1 and A2 are equal providing L1=L2 and B1=B2.
Area of Triangle
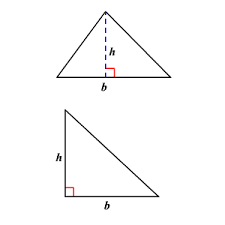
The area of a triangle is defined as the total space occupied by the three sides of a triangle in a 2-dimensional plane. The basic formula for the area of a triangle is equal to half the product of its base and height, i.e., A = 1/2 × b × h. This formula is applicable to all types of triangles, whether it is a scalene triangle, an isosceles triangle, or an equilateral triangle. It should be remembered that the base and the height of a triangle are perpendicular to each other.

Area of Rectangle
The area can be defined as the amount of space covered by a flat surface of a particular shape. It is measured in terms of the “number of” square units (square centimeters, square inches, square feet, etc.) The area of a rectangle is the number of unit squares that can fit into a rectangle. Some examples of rectangular shapes are the flat surfaces of laptop monitors, blackboards, painting canvas, etc. You can use the formula of the area of a rectangle to find the space occupied by these objects. For example, let us consider a rectangle of length 4 inches and width 3 inches.


Area of a rectangle Definition: Area occupied by a rectangle within its boundary is called the area of the rectangle.
What is Perimeter?
The perimeter of a shape is defined because of the total distance around the shape. Basically, it’s the length of any shape if it’s expanded in an exceedingly linear form. The perimeter of various shapes can match in length with one another depending upon their dimensions. The circle doesn’t have a perimeter it has the only circumference.
let us take an example, if a circle is formed of a metal wire of length L, then the identical wire we can use to construct a square, whose sides are equal in length.
Difference Between Area and Perimeter
Some formulas of area and perimeter
| Shape | Area | Perimeter | Terms |
|---|---|---|---|
| Square | A = a^2 | P = 4a | a = length of the side |
| Rectangle | A = l × w | P = 2(l + w) | l = length w = width |
| Parallelogram | A = b × h | P = 2(a+b) | a = side b=base h=vertical height |
| Triangle | A = ½ × b × h | S = a+b+c | b = base h = height a,b and c are the sides of the triangle |
| Circle | A = π × r2 | Circumference = 2πr | r = radius of the circle |
Examples
Example 1: If the length of the side of a square is 12 m. Then find its area and perimeter.
Solution: Given, side of square = 12 m
Area = side2 = 122 = 144 sq.m
Perimeter = 4 side = 4 x 12 = 48 sq.cm.
Example 2: The length of the rectangular plot is 13 yards and the width is 9 yards. Find the area and perimeter of the plot.
Solution: Given, Length = 13 yards
Width = 9 yards
Therefore, Area = length x width = 13 x 9 = 117 sq. yards
Perimeter = 2 (length + width) = 2 x (13 + 9) = 2 x 22 = 44 yards.




